Help

Some concepts used in the DLMF Standard Reference Tables (DLMF Tables) web service are clarified in the following:

base

Input and output are currently only provided using base 10. Support for other bases may be included in the future.

input digits

Numbers that users provide in the forms or in uploaded data files are assumed to be exact as given. For example, the number $0.333$ is assumed to be exactly $\frac{333}{1000}$ and not a truncation of $\frac{1}{3}$.

output digits

A user may request up to 500 output digits. By default, a strict high-precision enclosure (lower and upper bound) is displayed for each requested function value. For example, if the user requests $n$ digits, the computed function values are displayed in scientific notation with $n$ digits, plus five extra digits (displayed smaller), along with exclusive error bounds (digits after $\pm$). In most cases, this allows the user to determine the value to the desired number of digits using whatever rounding or truncation scheme preferred.

Alternatively, instead of an interval enclosure the user may explicitly choose that output values be displayed in one of the following rounding modes:

• –

  round to nearest (even)

• –

  round up (toward $+\mathrm{\infty }$)

• –

  round down (toward $-\mathrm{\infty }$)

• –

  round toward $0$

• –

  round away from $0$

comparisons

When a user uploads a file containing $n$-digit function values for comparison, a table is constructed with computed reference values alternating with the values provided by the user. The approximate relative error is also shown. As described above, reference values are either computed to $n+5$ digits, or displayed with the rounding mode selected by the user. Differences between corresponding digits of the reference values and uploaded values are highlighted in either yellow (warning) or red (error) as explained below.

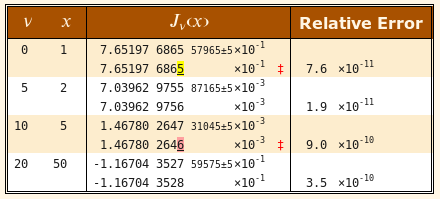
If the user selects a comparison based on interval mode, the upper and lower error bounds associated with each reference value form a sharp interval enclosure for the reference function evaluation. To accommodate the rounding or truncation used to produce the uploaded values, we take the floor of the left endpoint (round toward $-\mathrm{\infty }$) and the ceiling of the right endpoint (round toward $+\mathrm{\infty }$) to n digits.

If the user’s value falls outside this expanded interval, incorrect digits are highlighted in red and the user will see the message ’Value not in interval enclosure at requested precision’ when the cursor is placed near the dagger adjacent to the uploaded number.

If the user’s value falls within the expanded interval (endpoints included), but does not match the round to nearest (even) value computed from the reference value, digits in question are highlighted in yellow and the message will state ’Value not equal to round to nearest’.